Electron probability density functions for a hydrogen atom
I created a program with Visual Studio 2022 to plot the probability density functions of an electron in a hydrogen atom using WPF, Material Design In XAML Toolkit, MahApps.Metro, Prism, and ScottPlot.
This program plots the values of the probability density functions on the xz plane at y=0. The length of the xz-axis is shown in a heat map, with the Bohr radius set to 1.
1. I uploaded the executable file for Windows 10 and Windows 11 on the following page.
https://www.leafwindow.com/softwares/msix/hydrogen-atom-electron-probability-density/
The procedure to install the executable file is the same as this page.
I confirmed that it works on Windows 11 Version 22H2. I specified Windows 10 Version 1803 to Windows 11 Version 22H2 as the target OS when creating the MSIX package. It will work on Windows 10 Version 1803 or later.
2. The source code has been uploaded at the following github repository.
https://github.com/fukagai-takuya/quantum-mechanics-practice
3. About this program
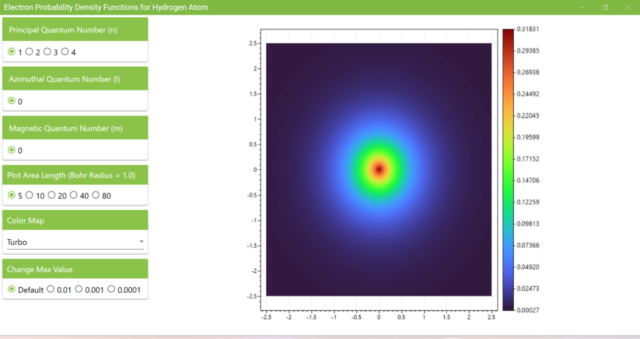
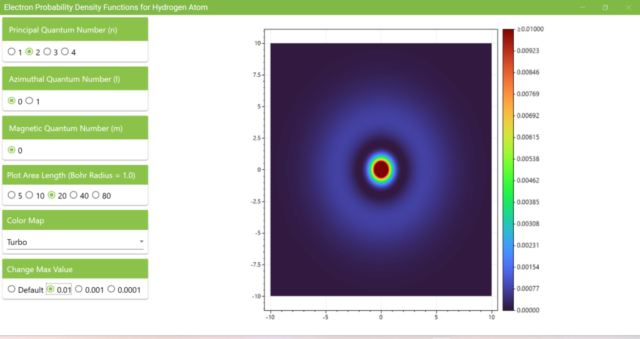
3.1. After launching the program, you will see the probability density function of an electron on the xz plane with the Principal Quantum Number (n) as 1, the Azimuthal Quantum Number (l) as 0, and the Magnetic Quantum Number (m) as 0.
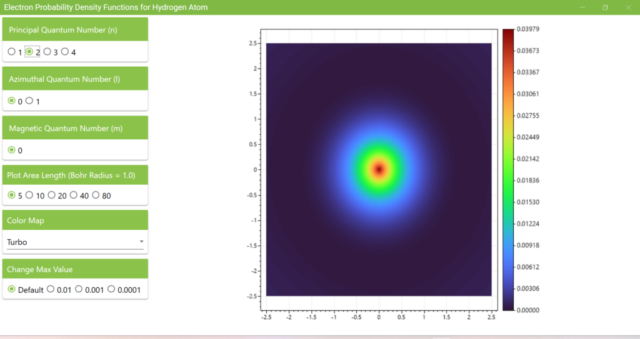
3.2. The figure shows the probability density function when the principal quantum number (n) is set to 2. Although the maximum value of the vertical bar next to the heatmap changes, the distribution of colors on the heatmap remains almost the same as n=1, l=0, m=0.
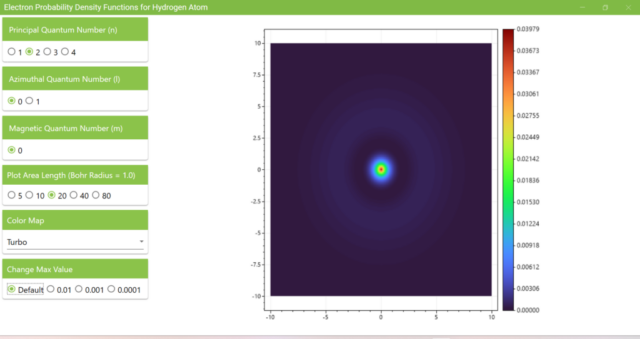
3.3. If you set the xz axis length (Plot Area Length) to 20 with the Bohr Radius as 1, you can see that the probability density is lower around the Bohr Radius of 2, and it increases slightly with the radius greater than 2.
3.4. The figure below shows the heatmap with the maximum value changed to 0.01 (Change Max Value). It can be seen more clearly that the probability density is lower around Bohr radius of 2. This differs significantly from the distribution for the quantum numbers n=1, l=0, m=0.
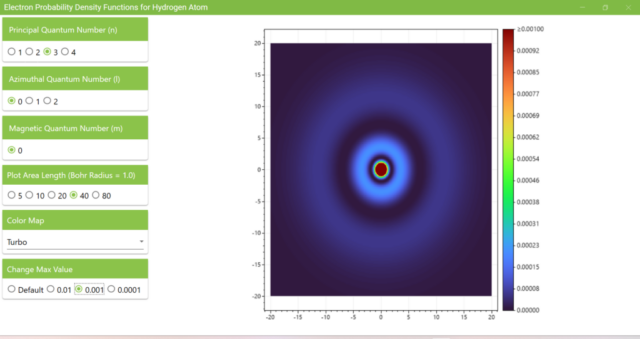
3.5. Heatmap for quantum numbers n=3, l=0, m=0. The length of the xz axis is 40 and the maximum value of the heatmap is 0.001.
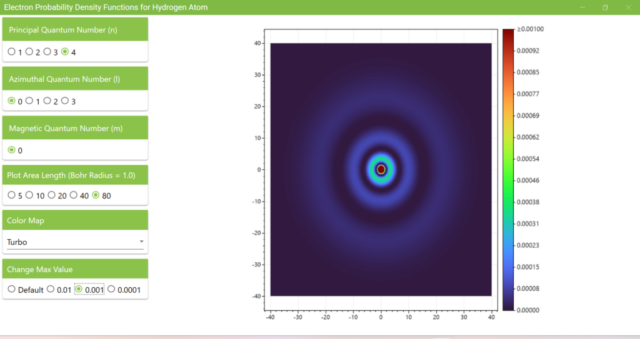
3.6. Heatmap for quantum numbers n=4, l=0, m=0. The length of the xz axis is 80 and the maximum value of the heatmap is 0.001.
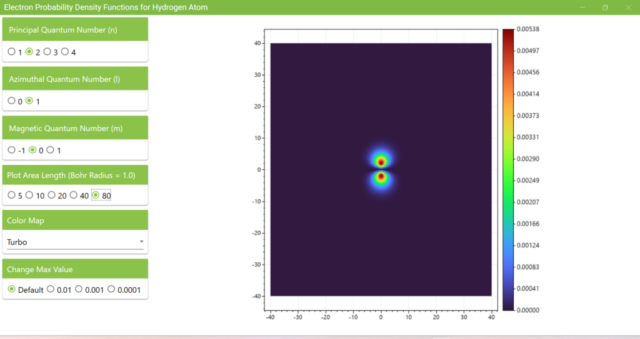
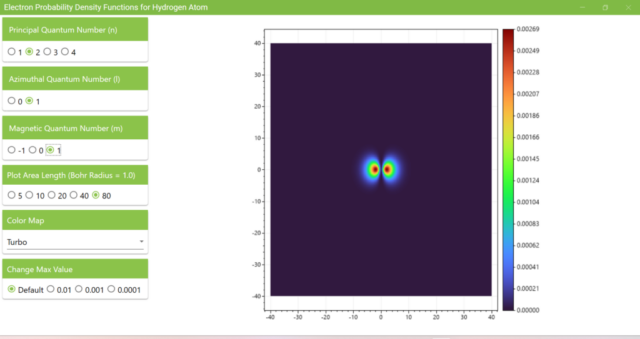
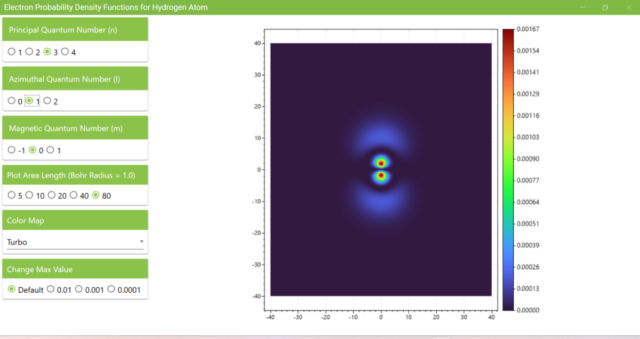
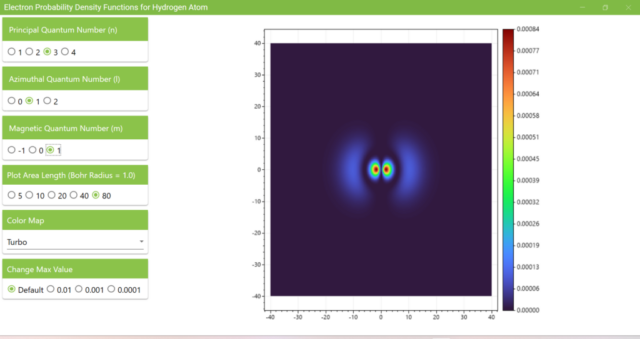
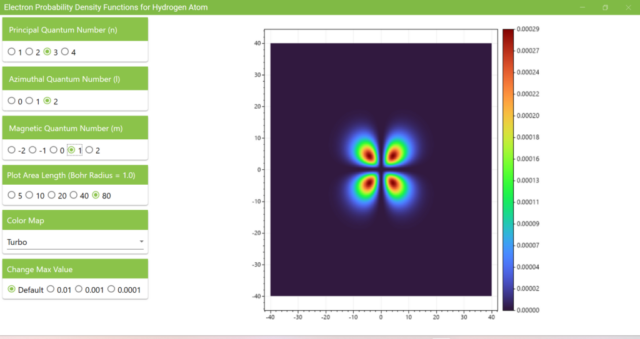
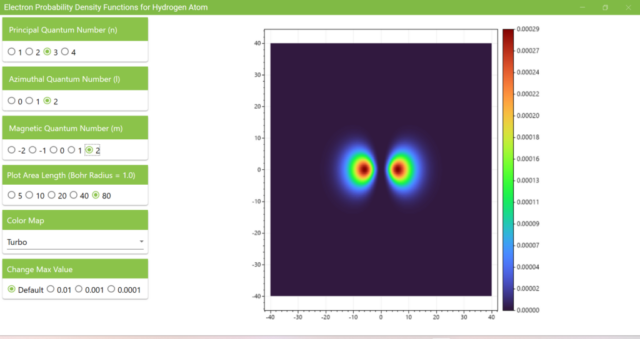
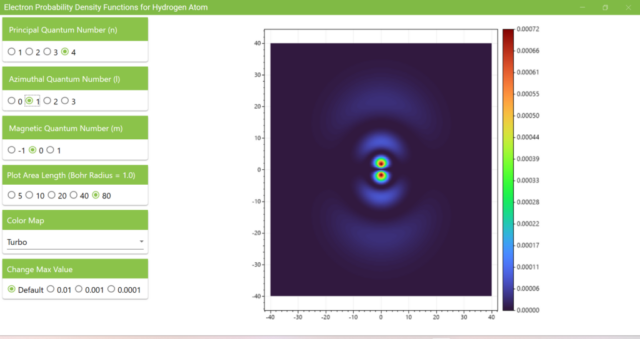
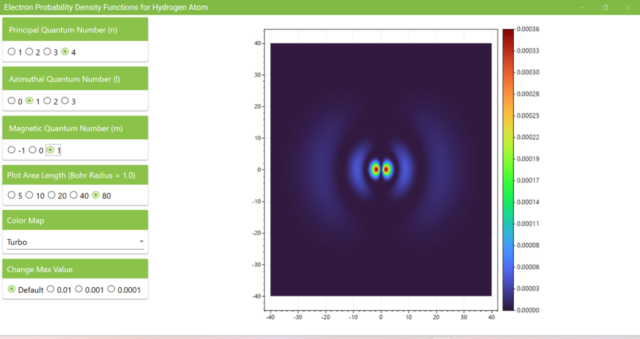
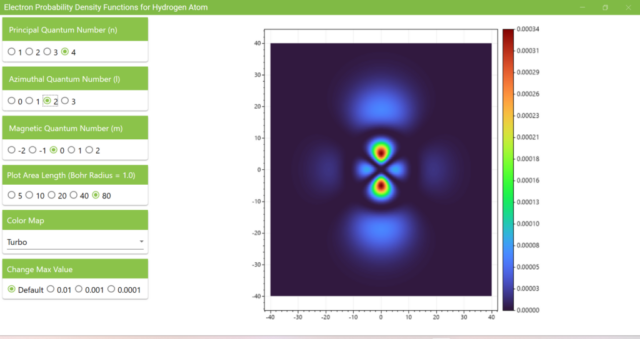
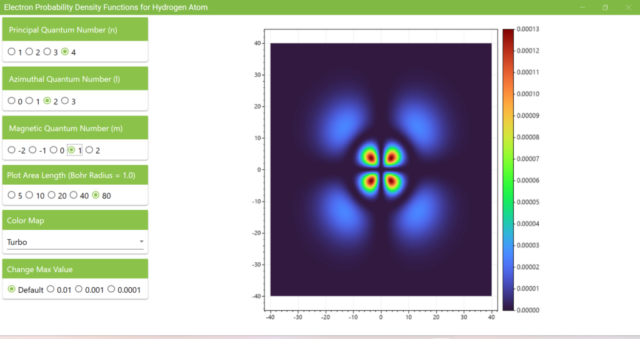
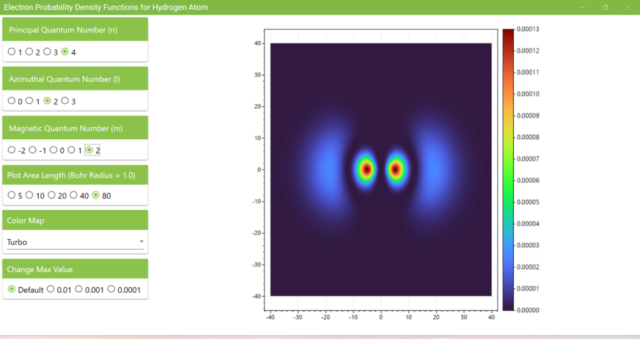
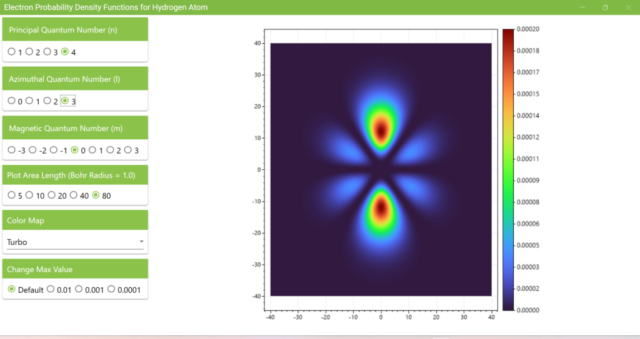
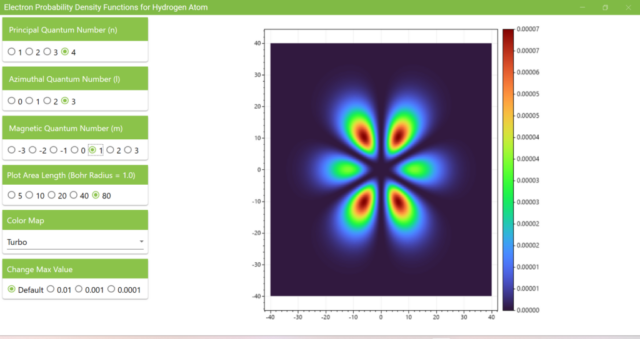
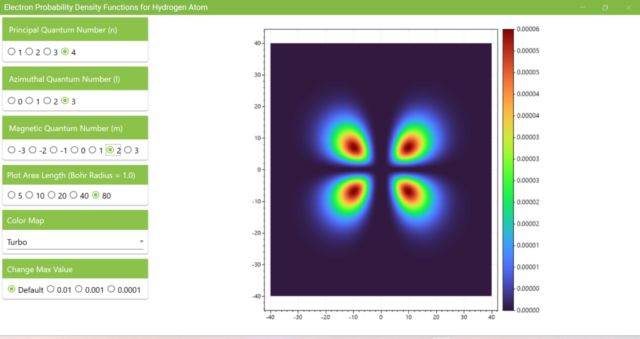
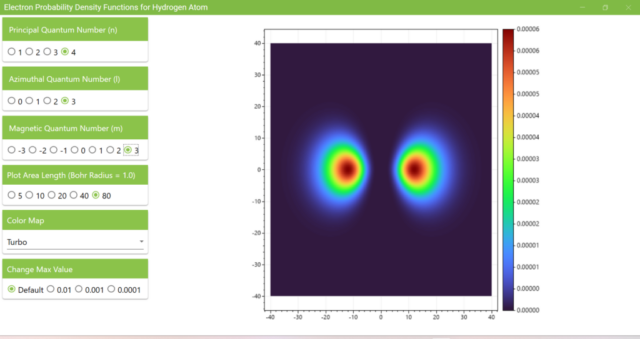
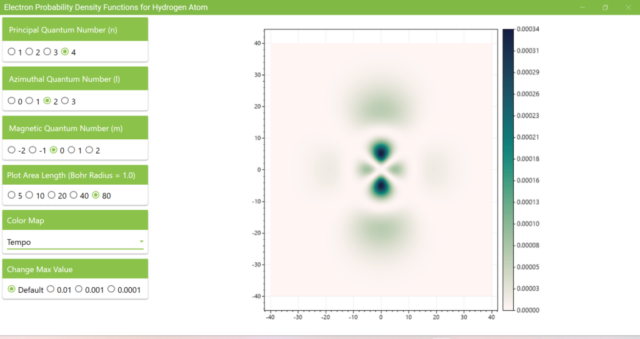
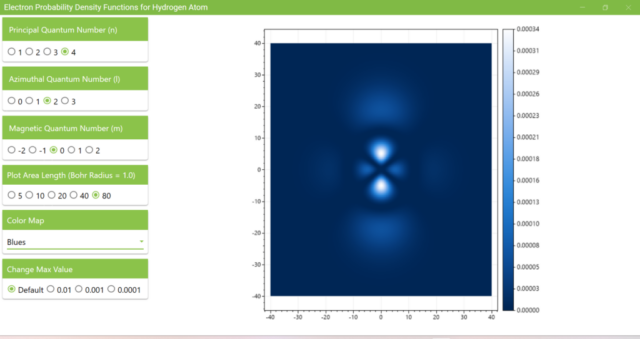
3.7. These are the probability density functions obtained when the principal quantum number n is changed to 2, 3, or 4 and the azimuthal quantum number l is set to a non-zero value. The magnetic quantum number m is set to 0 and positive integers only; the probability density function obtained here is the same when m is set to a negative integer as when a positive integer of equal absolute value is set.
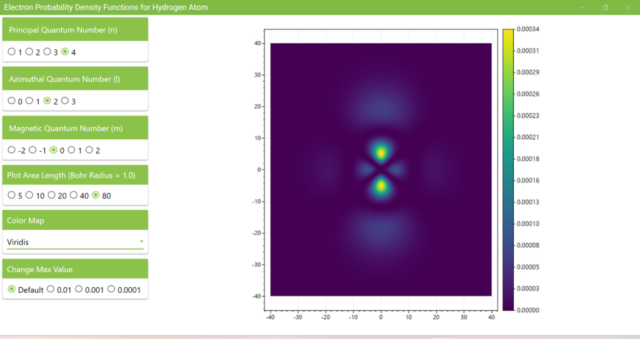
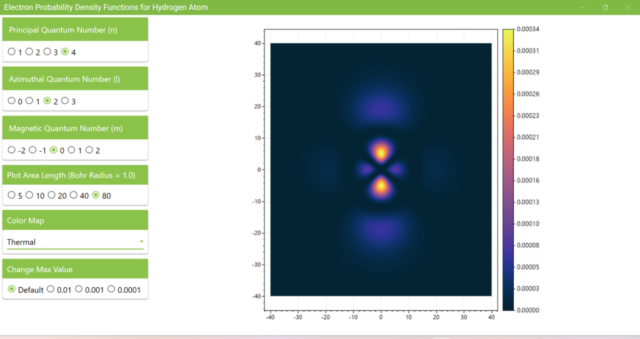
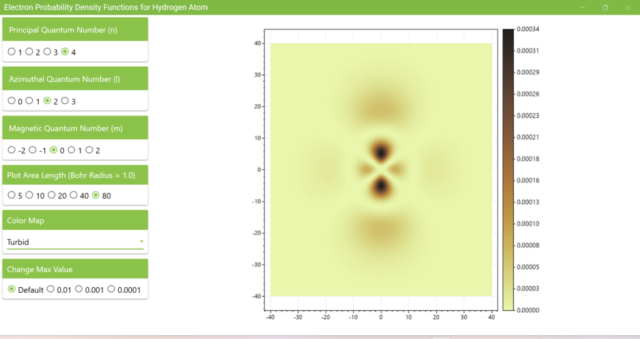
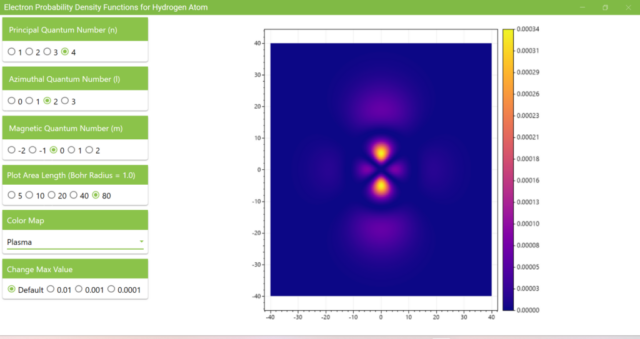
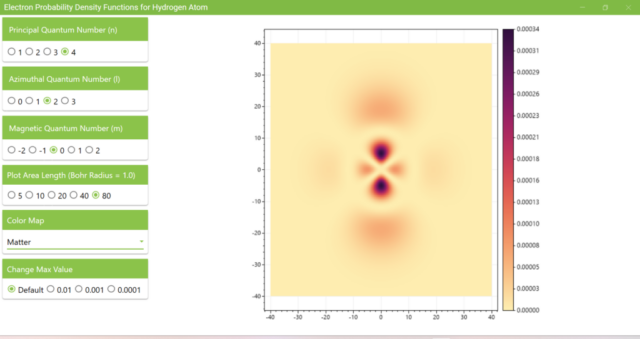
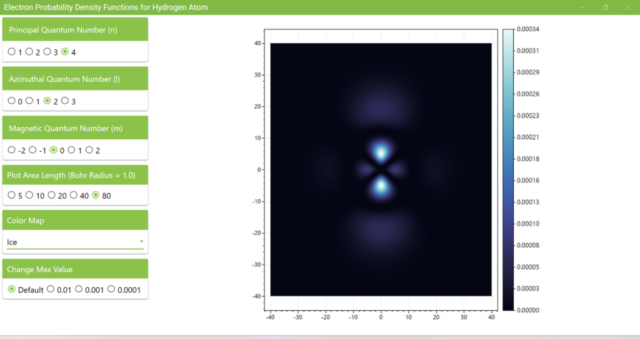
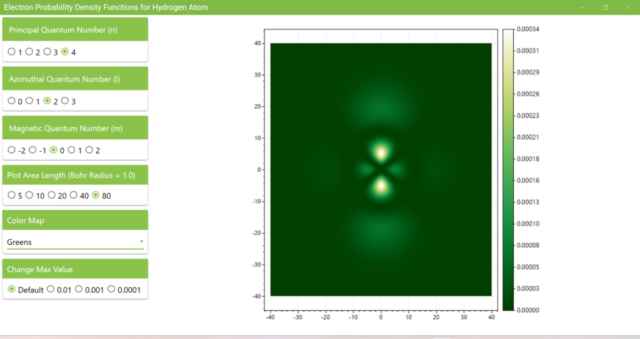
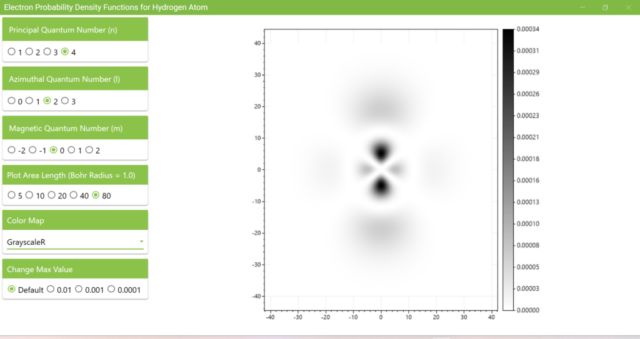
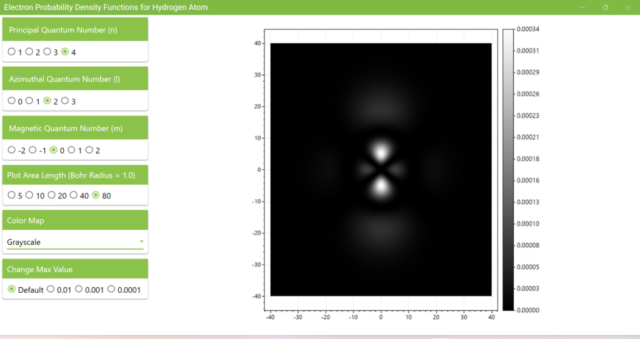
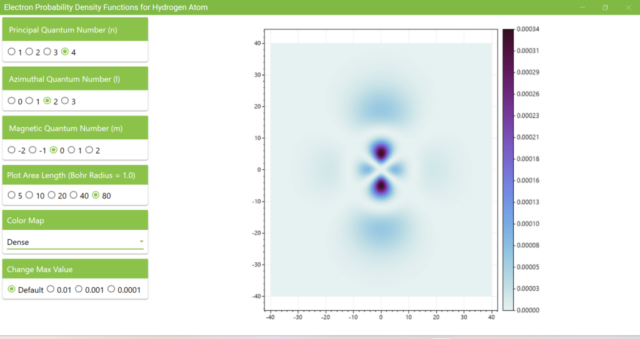
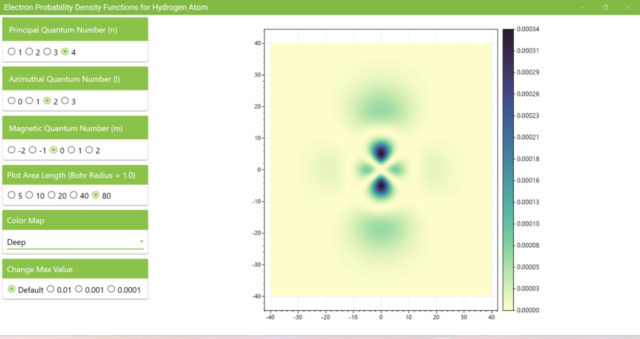
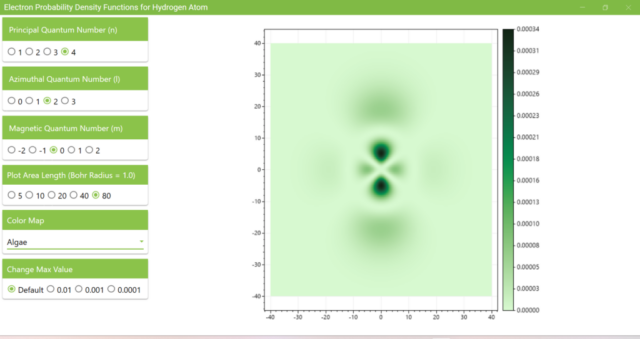
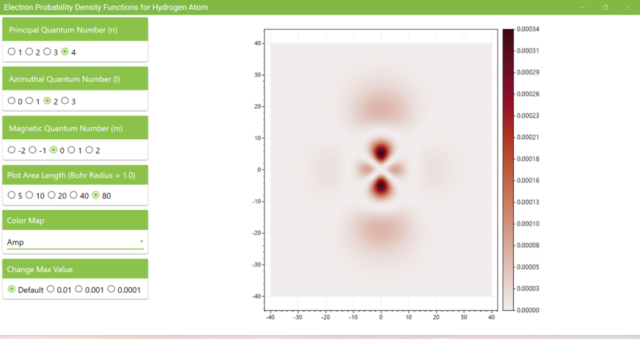
3.8. The figure plots the values of the probability density function on the xz plane for the principal quantum number n=4, the azimuthal quantum number l=2, and the magnetic quantum number m=0 by selecting the various color maps provided with ScottPlot. The colors change as you change the Color Map selection in the application.